第 3 章 对词与文档频率进行分析:tf-idf
文本挖掘与自然语言处理的一个中心问题是如何量化一个文档的内容。我们可以通过观察组成文档的词做到这一点吗?一个词的重要性的测度可以是其 词频(term frequency,tf),一个词在一个文档中出现的频率,我们在章 1 中已经检查过了。然而,一个文档中有些词出现了很多次但可能并不重要;在英语中,这些词很可能是诸如“the”“is”“of”之类。我们可以通过加入停止词列表的方法在分析前就把这些词去掉,但是这些词中的某些词可能在有的文档中比另一些更重要。用停止词列表调整常用词词频的方法还不够精巧。
另一种方法是观察一个术语在一组文档中的 逆向文档频率(inverse document frequency,idf),可降低常用词的权重并提高不很常用的词的权重。可以将 idf 与 tf 合并来计算一个术语的 tf-idf(把这两个量相乘),从而用一个术语不常见的量度来调整其频率。
The statistic tf-idf is intended to measure how important a word is to a document in a collection (or corpus) of documents, for example, to one novel in a collection of novels or to one website in a collection of websites.
这是条经验法则,是启发性质的量化;尽管可以验证 tf-idf 在文本挖掘、搜索引擎等应用中有效,信息理论专家认为其理论基础尚薄弱。任意给定的术语的逆向文档频率定义为:
\[idf(\text{术语}) = \ln{\left(\frac{n_{\text{文档的数量}}}{n_{\text{含有术语的文档的数量}}}\right)}\]
如果上面的公式看不清楚,可以在其上点击右键,选择 Math Settings -> Math Renderer -> HTML-CSS 或其它合适的选项。有时候 MathJax 默认选项对中文支持不佳。
我们可以如同章 1 中描述的那样使用 tidy 数据原则进行 tf-idf 分析,使用一致、有效的工具来量化不同术语对一组文档中的一个文档的重要程度。
3.1 《红楼梦》中的词频(tf)
从查看词频开始,然后才是 tf-idf。我们首先使用 dplyr 的功能,如 group_by() 和 join()。《红楼梦》中最常用的词有哪些?(为了后面计算 tf-idf,我们需要多个文档,因此把《红楼梦》按每二十章一部分共分为六个文档。)
library(dplyr)
library(stringr)
library(tidytext)
load("data/hongloumeng.rda")
# 无需移除停止词
cutter <- worker(bylines = TRUE)
chapter_words <- hongloumeng %>%
mutate(linenumber = row_number(),
chapter = paste("第",
1 + cumsum(str_detect(text, "^第[零一二三四五六七八九十百 ]*([二四六八 ]+十|零) ?一回")),
"部分")) %>%
mutate(text = sapply(segment(text, cutter), function(x){paste(x, collapse = " ")})) %>%
ungroup() %>%
unnest_tokens(word, text) %>%
count(chapter, word, sort = TRUE) %>%
ungroup()
total_words <- chapter_words %>%
group_by(chapter) %>%
summarize(total = sum(n))
chapter_words <- left_join(chapter_words, total_words)
chapter_words## # A tibble: 47,776 x 4
## chapter word n total
## <chr> <chr> <int> <int>
## 1 第 3 部分 了 3618 98766
## 2 第 4 部分 了 3586 107844
## 3 第 2 部分 了 3191 91765
## 4 第 6 部分 了 3126 87024
## 5 第 5 部分 了 3013 87281
## 6 第 4 部分 的 2807 107844
## 7 第 6 部分 的 2801 87024
## 8 第 3 部分 的 2745 98766
## 9 第 5 部分 的 2478 87281
## 10 第 2 部分 的 2424 91765
## # ... with 47,766 more rows此 chapter_words 数据框中每个词-部分之组合一行;n 是该词在该部分中出现的次数,total 是该部分全部词的数量。有最高 n 值的通常怀疑对象显然包括了“了”和“的”等。在图 3.1中,可以看到每部分中 n/total 的分布,一个词在一部分中出现的次数除以该部分所有术语(即词)的总量。这就是词频的含义。
ggplot(chapter_words, aes(n/total, fill = chapter)) +
geom_histogram(show.legend = FALSE) +
xlim(NA, 0.0009) +
facet_wrap(~chapter, ncol = 2, scales = "free_y")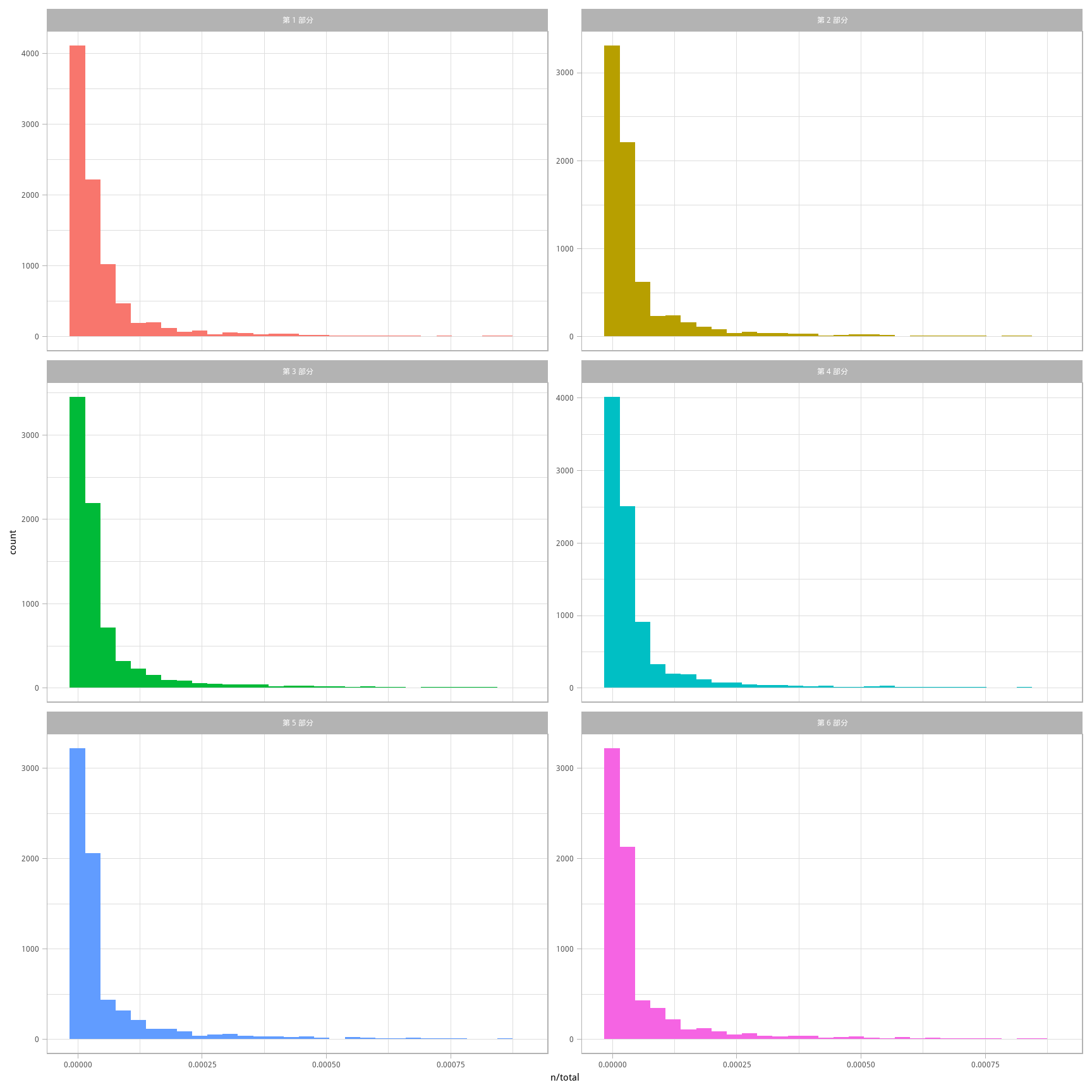
图 3.1: 《红楼梦》各部分的词频分布
每个部分的右侧都有很长的长尾(不够常见的词),在图中并未显示。这些图显示了所有部分都有相似的分布,即很多词出现得不多而较少词出现很频繁。
3.2 齐夫定律(Zipf’s law)
如图 3.1 所示的分布在语言中很典型。实际上,给出任何自然语言的语料(如一本书,来自网站的大量文本,或是大量口述),长尾分布的类型都如此常见,因此一个词的频率与其排名的关系一直是研究的对象;这种关系的一个经典版本叫做齐夫定律,来自一位20世纪美国语言学家乔治·齐夫。
Zipf’s law states that the frequency that a word appears is inversely proportional to its rank.
有了用来绘制词频的数据框,只要几行 dplyr 函数即可在《红楼梦》的各部分上检验齐夫定律。
freq_by_rank <- chapter_words %>%
group_by(chapter) %>%
mutate(rank = row_number(),
`term frequency` = n/total)
freq_by_rank## # A tibble: 47,776 x 6
## # Groups: chapter [6]
## chapter word n total rank `term frequency`
## <chr> <chr> <int> <int> <int> <dbl>
## 1 第 3 部分 了 3618 98766 1 0.0366
## 2 第 4 部分 了 3586 107844 1 0.0333
## 3 第 2 部分 了 3191 91765 1 0.0348
## 4 第 6 部分 了 3126 87024 1 0.0359
## 5 第 5 部分 了 3013 87281 1 0.0345
## 6 第 4 部分 的 2807 107844 2 0.0260
## 7 第 6 部分 的 2801 87024 2 0.0322
## 8 第 3 部分 的 2745 98766 2 0.0278
## 9 第 5 部分 的 2478 87281 2 0.0284
## 10 第 2 部分 的 2424 91765 2 0.0264
## # ... with 47,766 more rows这里的 rank 列显示了频率表内每个词的排名;由于表已经按 n 排序,我们可以用 row_number() 来确定排名。之后,我们可以按与之前一样的方式计算词频。要可视化齐夫定律,通常以排名为横坐标,词频为纵坐标,均使用对数比例。这种方式得到的逆向比例关系图像有稳定的负斜率。
freq_by_rank %>%
ggplot(aes(rank, `term frequency`, color = chapter)) +
geom_line(size = 1.1, alpha = 0.8, show.legend = FALSE) +
scale_x_log10() +
scale_y_log10()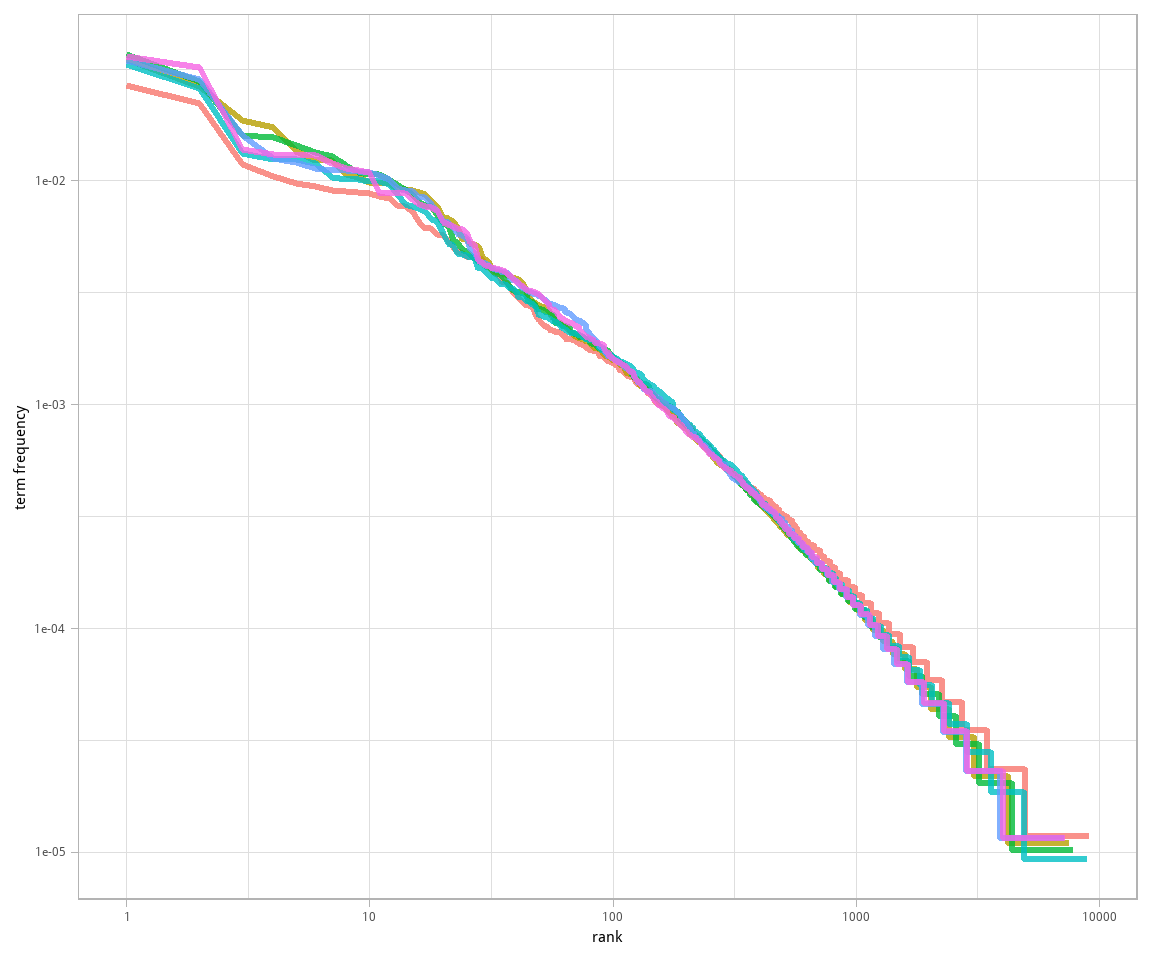
图 3.2: 《红楼梦》中的齐夫定律
注意,图 3.2 中的坐标轴为对数-对数关系。可以看出,《红楼梦》的六个部分都很相似,排名与频率间的关系呈现负斜率,然而并不十分恒定。也许我们可以把这条线分成比方说三段,呈现为幂定律。来看一下排名区间位于中段的幂指数如何。
rank_subset <- freq_by_rank %>%
filter(rank < 500,
rank > 10)
lm(log10(`term frequency`) ~ log10(rank), data = rank_subset)##
## Call:
## lm(formula = log10(`term frequency`) ~ log10(rank), data = rank_subset)
##
## Coefficients:
## (Intercept) log10(rank)
## -0.899 -0.964经典版本的齐夫定律有
\[\text{频率} \propto \frac{1}{\text{排名}}\] 而我们实际上已经得到了接近 -1 的斜率。把拟合的幂定律绘制到图 3.3 里看看是什么样。
freq_by_rank %>%
ggplot(aes(rank, `term frequency`, color = chapter)) +
geom_abline(intercept = -0.90, slope = -0.96, color = "gray50", linetype = 2) +
geom_line(size = 1.1, alpha = 0.8, show.legend = FALSE) +
scale_x_log10() +
scale_y_log10()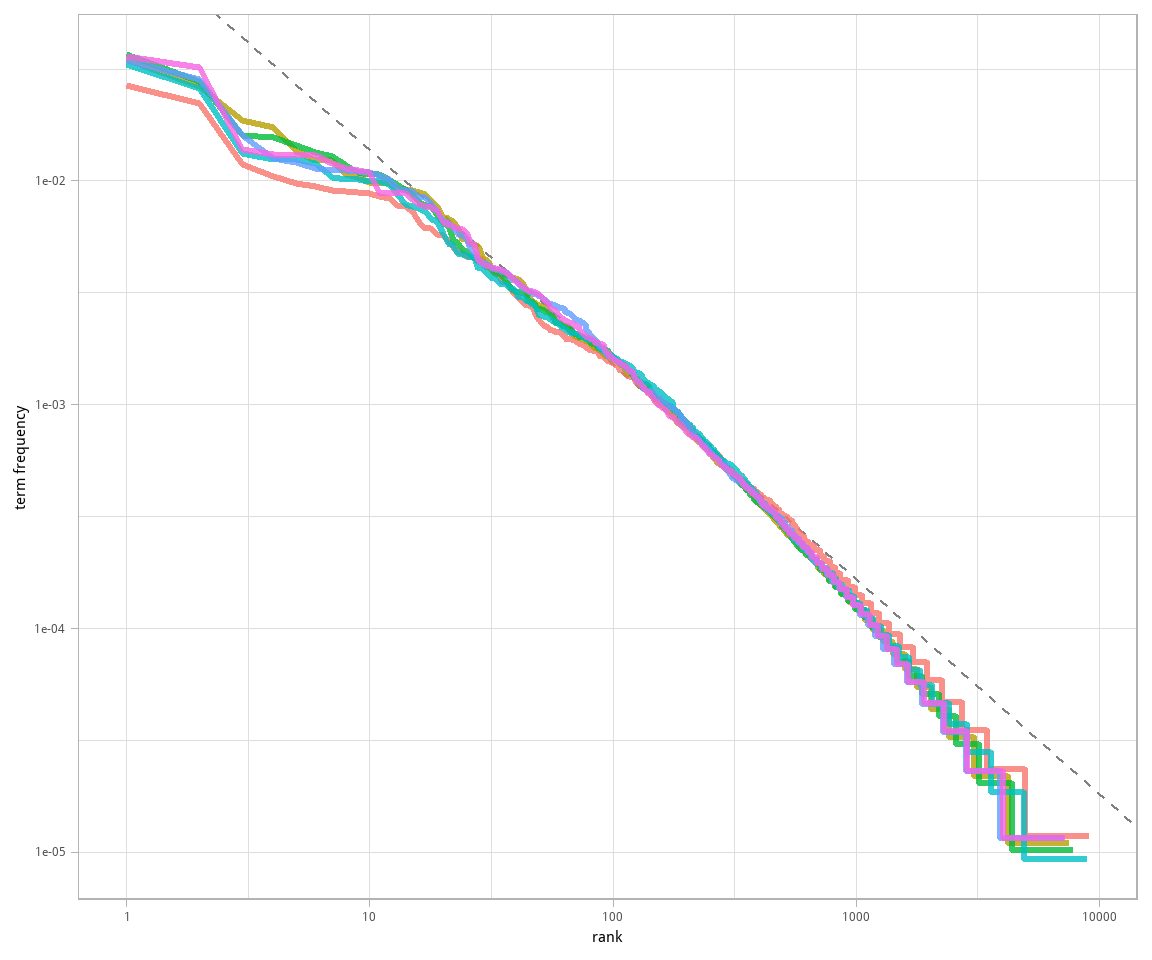
图 3.3: 带有拟合指数的《红楼梦》中的齐夫定律
我们在《红楼梦》的语料中发现了和经典版本齐夫定律接近的结果。在高排名端的情况并不特别,很多语言都如此;语料中通常含有比单一幂定律的预测更少的不常见词。在低排名端的变化较不寻常。曹雪芹用得最多的词的占比低于很多其它语料。这种分析可以扩展到比较不同作家,或是比较不同的文本集合;用 tidy 数据原则很容易做到。
3.3 bind_tf_idf 函数
tf-idf 的理念是通过在多个文档的集合(即语料)中降低常用词权重并提高不常用词权重以找到对于每个文档的内容更重要的词,在这个例子里,即包含所有部分的整部《红楼梦》。计算 tf-idf 尝试找到文本中重要(即普遍)但又不 过于 普遍。现在开始。
在 tidytext 包中的 bind_tf_idf 函数以一个 tidy 文本数据集作为输入,每文档每符号(术语)一行。一列(这里是word)含有术语/符号,一列含有文档(本例中为chapter),然后是必要的列,含有计数,每个文档含有每个术语多少次(本例中为n)。我们在前面为每个部分计算了 total,但 bind_tf_idf 函数并不需要;表只需含有每个文档中的所有词。
chapter_words <- chapter_words %>%
bind_tf_idf(word, chapter, n)
chapter_words## # A tibble: 47,776 x 7
## chapter word n total tf idf tf_idf
## <chr> <chr> <int> <int> <dbl> <dbl> <dbl>
## 1 第 3 部分 了 3618 98766 0.0366 0 0
## 2 第 4 部分 了 3586 107844 0.0333 0 0
## 3 第 2 部分 了 3191 91765 0.0348 0 0
## 4 第 6 部分 了 3126 87024 0.0359 0 0
## 5 第 5 部分 了 3013 87281 0.0345 0 0
## 6 第 4 部分 的 2807 107844 0.0260 0 0
## 7 第 6 部分 的 2801 87024 0.0322 0 0
## 8 第 3 部分 的 2745 98766 0.0278 0 0
## 9 第 5 部分 的 2478 87281 0.0284 0 0
## 10 第 2 部分 的 2424 91765 0.0264 0 0
## # ... with 47,766 more rows注意,这些极度常见的词的 idf 为0,因此 tf-idf 也是0。这些是在每一部分中都出现过的词,因此 idf (即1的自然对数)是0。在一个集合中的很多文档都出现的词,其逆向文档频率(以及 td-idf)就会非常低;这个方法就是这样降低常见词权重的。出现在集合中较少文档的词拥有较高的逆向文档频率。
来看一下在《红楼梦》各部分中高 tf-idf 的术语。
chapter_words %>%
select(-total) %>%
arrange(desc(tf_idf))## # A tibble: 47,776 x 6
## chapter word n tf idf tf_idf
## <chr> <chr> <int> <dbl> <dbl> <dbl>
## 1 第 4 部分 二姐 140 0.00130 0.693 0.000900
## 2 第 1 部分 智能 26 0.000304 1.79 0.000545
## 3 第 4 部分 尤 311 0.00288 0.182 0.000526
## 4 第 2 部分 劉姥姥 92 0.00100 0.405 0.000407
## 5 第 5 部分 蝌 80 0.000917 0.405 0.000372
## 6 第 6 部分 嗎 46 0.000529 0.693 0.000366
## 7 第 6 部分 勇 45 0.000517 0.693 0.000358
## 8 第 1 部分 水溶 16 0.000187 1.79 0.000336
## 9 第 5 部分 知縣 26 0.000298 1.10 0.000327
## 10 第 6 部分 爻 14 0.000161 1.79 0.000288
## # ... with 47,766 more rows基本都是专有名词,人名(包括称谓)和地名在不同部分中相当重要。这里的词没有在所有部分都出现的,因此是对于《红楼梦》语料每个部分的文本具有代表性的词。
Some of the values for idf are the same for different terms because there are 6 documents in this corpus and we are seeing the numerical value for ((6/1)), ((6/2)), etc.
图 3.4 是对这些高 tf-idf 词的可视化。
chapter_words %>%
select(-total) %>%
arrange(desc(tf_idf)) %>%
mutate(word = factor(word, levels = rev(unique(word)))) %>%
group_by(chapter) %>%
top_n(10) %>%
ungroup %>%
ggplot(aes(word, tf_idf, fill = chapter)) +
geom_col(show.legend = FALSE) +
labs(x = NULL, y = "tf-idf") +
facet_wrap(~chapter, ncol = 2, scales = "free") +
coord_flip()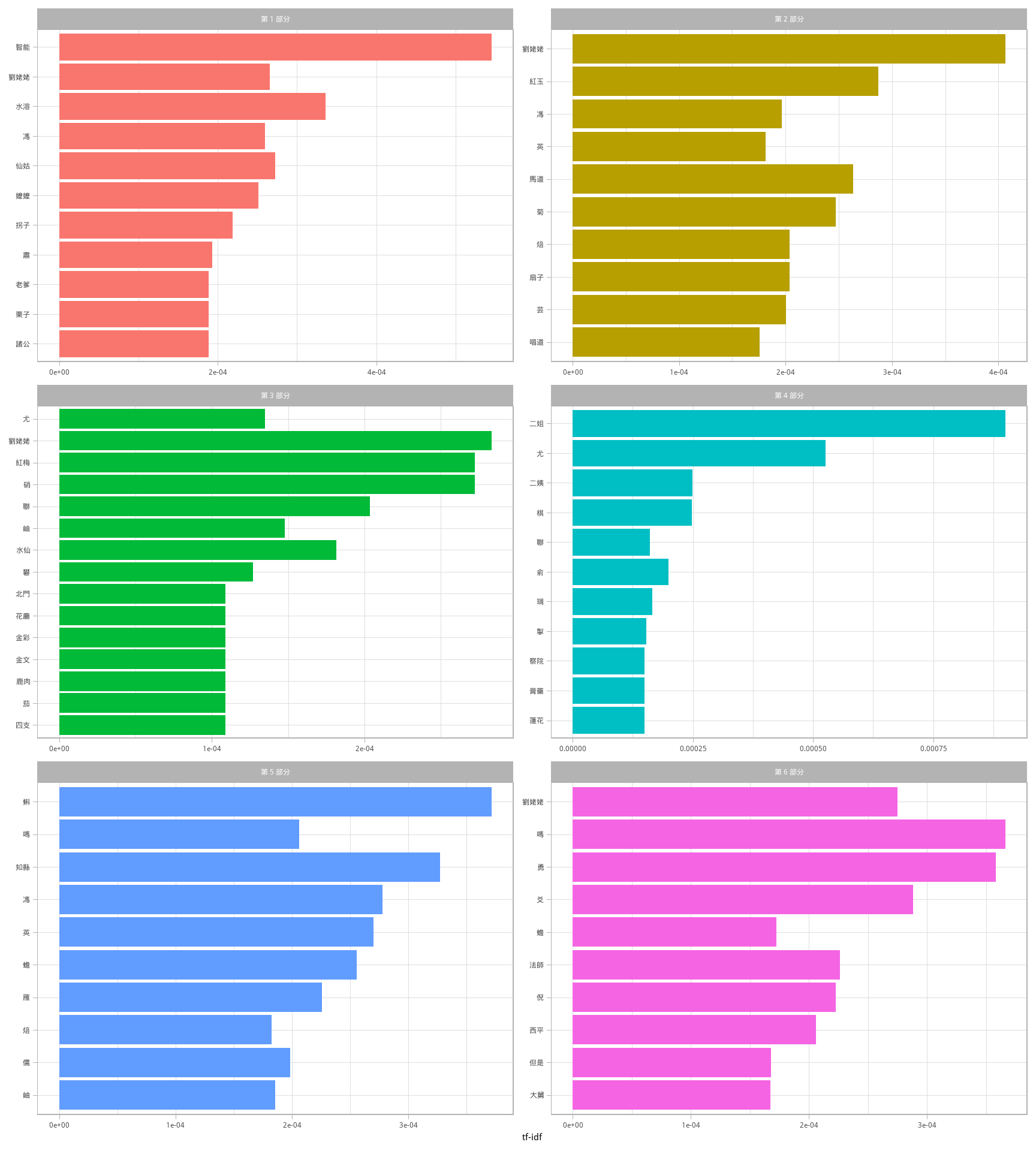
图 3.4: 《红楼梦》每个部分中 tf-idf 最高的词
图 3.4 中占据统治地位的依然是专有名词!由 tf-idf 度量找到的这些词对其所在的部分非常重要,多数读者当欣然同意。tf-idf 度量可以告诉我们《红楼梦》各部分语言相似,而区分不同部分的主要是专有名词,人名和地名,以及其它一些名词。这就是 tf-idf 的意义;识别出对多个文档的集合中的一个文档更重要的词。
3.4 科技文本语料
下面对另一种文档组成的语料进行分析,看看在不同集合的作品中什么术语重要。实际上,我们将彻底离开小说和记叙文体的世界。从古登堡计划下载一些古代经典的技术文本,用 tf-idf 衡量一下这些作品里什么术语重要。下载劉徽《海島算經》、孫子《孫子算經》、沈括《夢溪筆談》和宋應星《天工開物》。
这组文本相当发散。尽管都是经典的技术性文本,但前后超越千年,时间跨度大,而且从数学到工程,同质性应该很低。但这不能阻挡我们进行下面的有趣实验!
library(gutenbergr)
stem <- gutenberg_download(c(26979, 24038, 27292, 25273),
meta_fields = "author")有了文本,我们使用 unnest_tokens() 和 count() 来找出每个词在每个文本中使用的次数。
# 无需移除停止词
cutter <- worker(bylines = TRUE)
stem_words <- stem %>%
mutate(text = sapply(segment(text, cutter), function(x){paste(x, collapse = " ")})) %>%
unnest_tokens(word, text) %>%
count(author, word, sort = TRUE) %>%
ungroup()
stem_words## # A tibble: 14,979 x 3
## author word n
## <chr> <chr> <int>
## 1 Shen, Kuo 之 2186
## 2 Shen, Kuo 為 981
## 3 Shen, Kuo 也 855
## 4 Shen, Kuo 其 826
## 5 Shen, Kuo 有 791
## 6 Song, Yingxing 者 787
## 7 Shen, Kuo 以 747
## 8 Shen, Kuo 者 725
## 9 Song, Yingxing 之 666
## 10 Song, Yingxing 其 641
## # ... with 14,969 more rows目前我们看到的只是原始计数;要记得这些文档长度不同。我们继续计算 tf-idf,然后在图 3.5 中可视化 tf-idf 值高的词。
plot_stem <- stem_words %>%
bind_tf_idf(word, author, n) %>%
arrange(desc(tf_idf)) %>%
mutate(word = factor(word, levels = rev(unique(word)))) %>%
mutate(author = factor(author, levels = c("Liu, Hui, 3rd/4th cent.",
"Sunzi, ca. 5th cent.",
"Shen, Kuo",
"Song, Yingxing")))
plot_stem %>%
group_by(author) %>%
top_n(15, tf_idf) %>%
ungroup() %>%
mutate(word = reorder(word, tf_idf)) %>%
ggplot(aes(word, tf_idf, fill = author)) +
geom_col(show.legend = FALSE) +
labs(x = NULL, y = "tf-idf") +
facet_wrap(~author, ncol = 2, scales = "free") +
coord_flip()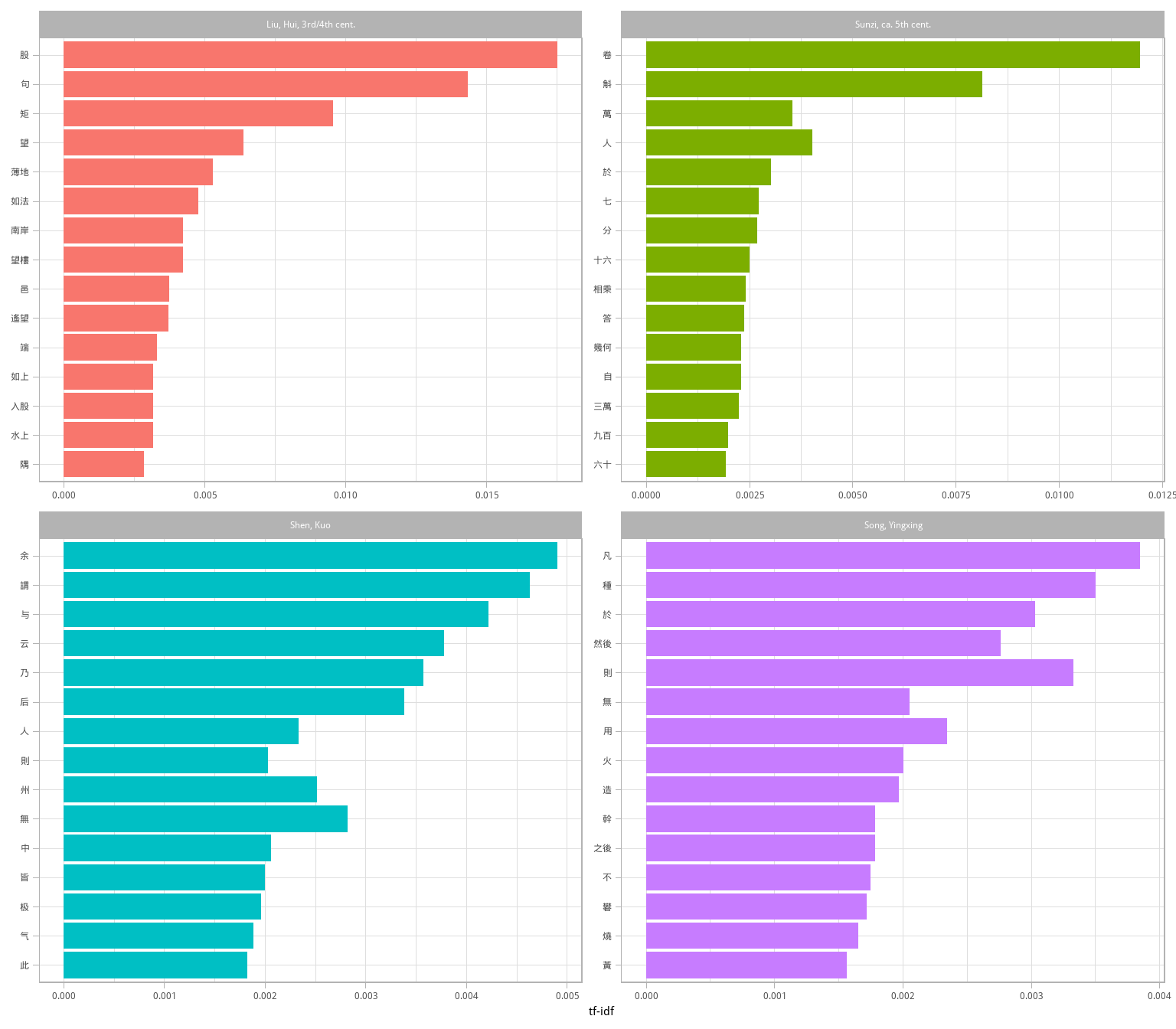
图 3.5: 每个科技文本中 tf-idf 最高的词
这个结果已经足够有趣。但具体数字在这里也许不是重点,我们可以尝试用 anti_join() 移除掉纯数字词。
library(stringr)
mystopwords <- stem_words %>%
filter(str_detect(word, "^[A-Za-z0-9零一二三四五六七八九十百千萬]+$")) %>%
select(word) %>%
as.data.frame()
stem_words <- anti_join(stem_words, mystopwords, by = "word")
plot_stem <- stem_words %>%
bind_tf_idf(word, author, n) %>%
arrange(desc(tf_idf)) %>%
mutate(word = factor(word, levels = rev(unique(word)))) %>%
mutate(author = factor(author, levels = c("Liu, Hui, 3rd/4th cent.",
"Sunzi, ca. 5th cent.",
"Shen, Kuo",
"Song, Yingxing")))
plot_stem %>%
group_by(author) %>%
top_n(15, tf_idf) %>%
ungroup() %>%
mutate(word = reorder(word, tf_idf)) %>%
ggplot(aes(word, tf_idf, fill = author)) +
geom_col(show.legend = FALSE) +
labs(x = NULL, y = "tf-idf") +
facet_wrap(~author, ncol = 2, scales = "free") +
coord_flip()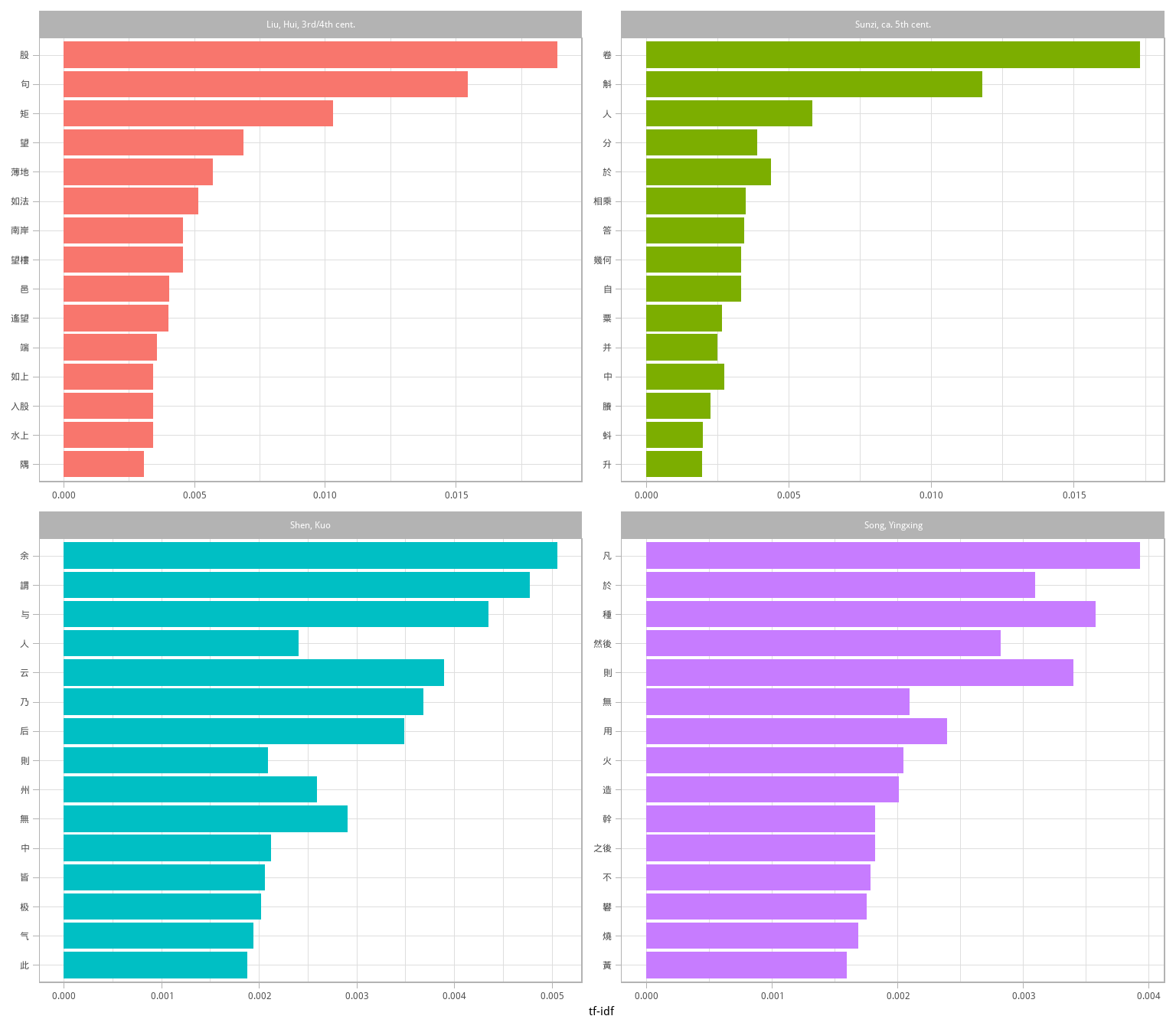
图 3.6: 每个科技文本中 tf-idf 最高的词
从图 3.6 中可以得出一些结论,如《天工開物》包括了工匠操作的具体步骤;算术方面,劉徽似乎更关注楼台高度、水土面积的计算等,而《孫子算經》则有更多度量粮食的问题。
3.5 小结
使用词频和逆向文档频率让我们能够找出多个文档的集合中的一个文档的特征词,无论文档是小说、科技文本还是网页。探索词频本身可以让我们洞见在自然语言的集合中语言是如何被使用的,而 dplyr 功能如 count() 和 rank() 给了我们得出词频的工具。tidytext 包使用了与 tidy 数据原则一致的 tf-idf 实现,让我们可以看到词在一组文档语料的每个文档中的重要性是多么不同。